제품 정보

- 제품 정보
- 열전냉각
- 열전냉각 Concept
- 성능지수
열전냉각 Concept
열전냉각Concept_ 성능지수(Z, figure-of merit)
Fi.2-5에 나타낸 전자냉각 및 발전 분야에 응용되는 열전모듈의 에너지 변환효율은 n형솨 p형 소자에 의해 이루어지는 conple의 수와 각 소자들의 열전특성에 의존하면, 우수한 열전특성을 갖는 소자를 사영할떄 모듈의 크기를 줄일 수 있습니다. ㅇ려전 특성은 각 재료의 Seebeck 계수, 전기비저항 및 열전도도가 미치는 영향에대하ㅐ서 살펴보기로 하자. fig.2-5와 같이,같이, 길이 단면적, Seebeck 계수 전기저항 및 열전도도가 각각 IA, sB, αB, αA, κB인 열전재료 A와 B를 이용하여 전기적으로는 직렬로, 열적으로는 병렬로 회로를 구성하여 모듈 양단의 온도차를 △T(=Th-Tc)로 유지하였다. 이때 모듈의 고온 단에서 흡수되는 열량 Qα 와 joule열의반인 (1/2)QJ와의 합이 Peltier 효과에 의한 열QP와 열전도에 의한 방출되는 열량 QK의 합과 갗으므로 식(207)과 같은 관계가 성립된다.
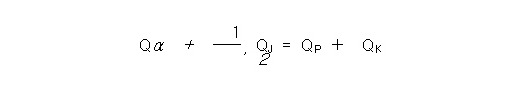
[식( 2.7 )]
식( 2.7 )에서 Peltier 효과에 의한 열량은 식(2.4)와 Ohm의 법칙에 의해 식(2.8)과 같이 나타낼 수 있습니다.
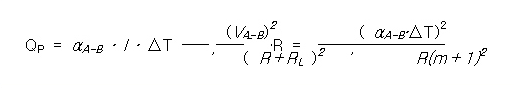
[식( 2.9 )]
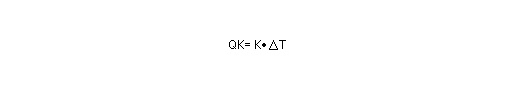
[식( 2.10 )]
여기서, K는 모듈에서 두 접점사이의 열전도율입니다. 식(2.8)~(2.10)을 대입하여 식(2.7)을 Qα에 대하여 정리하면 다음과 같다.
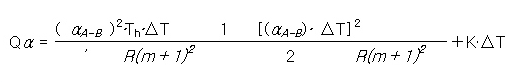
[식( 2.11 )]
또한, 온도차 △T에 의해 발생하는 전력 P는 다음과 같다.
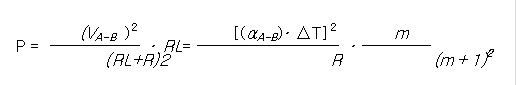
[식( 2.12 )]
짜라서, 열전발전 효율 η는 다음과 같이 나타낼 수 있습니다.
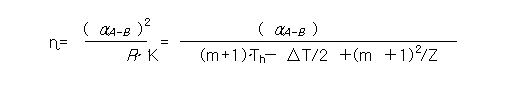
[식( 2.13 )]
식(2.13)에서 Z는 다음과 같다.
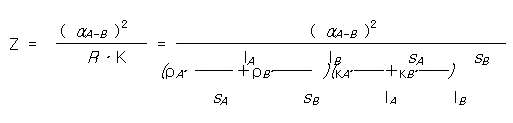
[식( 2.14 )]
식(2.14)에서 효율이 최대가 되는 m의 값 mopt=M에 대하여 정리하면,
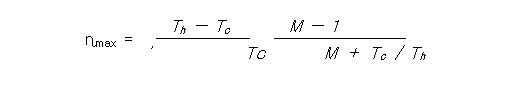
[식( 2.16 )]
로 주어지며, 식(2.15)에 따른 최대 효율 ηmax는 다음과 같이 나타낼 수 있습니다.
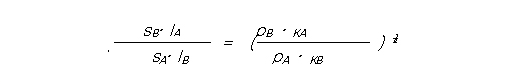
[식( 2.17 )]
식(2.15)와 식(2.16)에서 알 수 있듯이, 열전변환 효율을 크게 하기 위해서 Z의 값을 크게 해야합니다. 식(2.14)에서 (R.K)항이 작아야 하므로 다음식이 성립되어야 합니다.
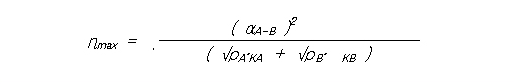
[식( 2.16 )]
식(2.17)의 조건이 만족될때, 식(2.14)는 다음과 같이 나타낼 수 있습니다.
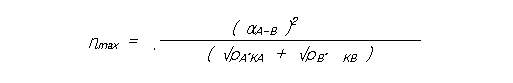
[식( 2.16 )]
이때 Z는 Seebeck 계수 α, 전기비저항 ρ및 열전도 k의 재료정수만으로 결정되며, 하나의 재료에대해서도 다음과 같이 나타낼 수 있습니다.
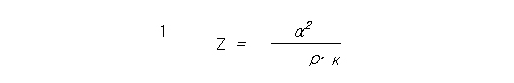
[식( 2.19 )]
즉 열전재료의 에너지 변환효율을 제대로 하려면 다음의 3가지 요소를 만족해야만 하며[18.19], Z를 성능지수(figure-of-merit)라고하여 열전재료의 양호도를 나타내는데 쓰여진다.
- ① 소자에 형성된 온도차는 클수록 좋으므로 열전도도(k0)가 작을 수록 좋다.
- ② 출력전압은 클 수록 좋기때문에 Seebeck 계수(α)는 클수록 좋다.
- ③ 큰 툴력을 내기 위해서 내부저항과 소자의 전기비저항(ρ)은 적을 수록 좋다.
Peltier 효과를 이용한 전자냉각의 경우에서도 이론적 고찰은 열전발전과 거의 유사하며, 마찬가지로 냉각효율울 크게 하려면 성능지수 Z를 크게 해야합니다.
성능지수의 최적조건
열전재료의 성능의 척도는 Z(Figure of Merit)로 나타내며, 성능지수는 Seebeck 계수(α), 비저항(ρ) 및 열전도율 (k)의 관계로 주어진다.

[식( 3 - 29 )]
위의 식으로부터 높은 성능지수를 얻기 위해서 Seebeck꼐수가 높고 비저항과 열전도율이 낮아야하는 것을 알 수 있습니다. 그러아 이들의 물리정수는 독립적이 아니고 캐리어(carrier, 전자 또는 정공) 농도에 관계가 있어, 열전능과 비저항은 전자농도 n의 증가에따라 감소합니다. 또한 열전도율은 일반적으로 전자의 열전도율 kel와 격자의 열전도 율 kph로 되어 있고
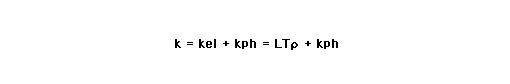
[식( 3 - 30 )]
나타낸다. 여기서 L은 로렌쯔 상수이며, ρ=(1/-p)은 전기전도도입니다.
그러나 kel은 캐리어농도 nc에 의존하지 않고 일정합니다. 성능지수가 최대 값을 나타내는 전자농도는 약 1025/m31의 영역이며 금속의 전자농도의 거의 1/1000입니다.이영역에서 ke은 단원소 반도체(Si,Ge) kph의 1%이하로 작고, 도한 화합물 반도체 kph의 10%정도입니다.
따라서 전자농도가 작은 영역에서 성능지수가 최대치를 보이는 전자농도는 출력인자(=α2σ)의 극대치와 비교해 거의 변화되지 않습니다. 이러한 정성적인 고찰로부터 성능지수가 큰 물질은 적당한 불순물의 첨가에 의해 캐리어농도를 적당히 제어하여야합니다.
또한 열전도율은 비데만프란쯔 법칙(Wiedeman-Franz Law)을 따르기때문에 비저항과의 독립된제어가 어렵지만,격자의 열전도율을 제어함으로써 전체 열전도율을 낮출 수 있습니다.따라서 높은 에너지를 갖는 고진동 포논(phonno)이 격자의 불규칙한 장소에서 강하게 산란되도록 조성 및 첨가제의 양을 변화시켜 이종재료의 고용체화에 의해 격자의 열전도율울 감소시킨다.
비교적 큰 경정입경을 갖는 다결정 체에서는 단위체적당 결정입계 면적이 작고 결정입계간의 거리도 입계산란의 자유행로 보다 크다 이 경우 온도 이하에서 열의 대부분을 운반하는 저진동 포논의 입계산란은 적고 이 효과에 의한 격자의 열전도율의 저하는 적다.
그러나 미세결정립은 결정이나 소결체에서는 입계산란에 의해 열전도율이 저하되는 효과가 생기고, 이러한 입계산란에의한 격자의 열전도율 κph은 결정입경의 감소에 반해 작게되며, 이 감소량은 결정이 작을수록 현저하다. 따라서 이종재료의 고용체화와 결정립 미세화로 격자열전도율을 감소시킴으로써 성능지수를 증가시킬 수 있습니다.
Bi2Te3(비쓰무쓰 텔레늄 합금)
Bi² Te³ 계 열전재료는 그림 5에서 보는바와 같이 단체금속과 dopsnt의 혼합물을 융용하여 일방향응고 시키는 방법과 인고트를 분말화 하여 얻은 분말을 이용하는 냉간 프레스 소결법과 열간프레스법에 의해 제조되고 있습니다.
일방향 응고제는 뛰어난 열전특성을 나타내고 있지만 온도구배, 성장속도등 제조조건이 어려울 뿐만 아니라 낮은 기계적 강도를 갖기 때문에 낮은 생산성과 소형의 소자 가공시 재료손실이 많은 단점을 갖고 있습니다. 성장속도등 제조조건이 어려울 뿐만 아니라 낮은 기계적 강도를 갖기 때문에 낮은 생산성과 소령의 소자 가공시 재료손실이 많은 단점을 갖고 있습니다. 이러한 단점을 해결하기 위하여 분말야금법이 도입되었습니다. 그러나 지금까지는 기계적 강도의 향상만을 고려하여, 분말을 냉간프레스한 성형체를 소결하는 냉간프레스법이 이용되어져 왔습니다. 그러나, Bi² Te³ 계 화합물은 특유의 구조민감성 때문에 냉간프레스한 변형에 의해서 열전능은 현저하게 작아지며 p형 Bi² Te³ 을 분말성형체로 하면 n형으로 변하며, 또한 열처리조건에도 민감하여 소결온도가 약간 달라도 p형으로 n형으로 변화하기 때문에 열처리조건의 설정에 어려운 점이 많습니다
더욱이 냉간프레스법에서는 고온소결에 의해서 소결체의 겉보기밀도와 이론밀도의 비를 90%이상으로 하면 결정립의 성장 및 칼코겐원소(Te,Se)의 증발에 의한 조성의 변화가 발생 하여 열전특성의 제어가 매우 곤란하였습니다.
따라서 냉간프레스법으로 제조한 Bi² Te³ 계 소결체는 시판되고 있는 일방향 ㅇ응고에 의한 용제재료의 열전성능지수(Z=2.5× 10-³ K-¹) 보다 높지 않으므로 현재까지 열전냉각, 가열용 재료로서 실용화되지 않고 있습니다.
한편, 열간프레스법에서는 압력을 가하면서 소결을 행하기 때문에 소결온도가 낮아도 90%이상의 소결체를 용이하게 제조할 수 있으며, 냉간프레스법에 비하여 저온에서 소결이 가능하여 결정립성장을 억제할수가 있습니다.
또한 Bi² Te³ 의 벽개면 이 c면이라는 점에 주목하여 열간프레스법에 의한 소결체의 가압방향에 각 결정립의 c축이 되도록 제조한 결과, 열전기적 수송현상에 있어서, 결정 대칭성을 반영한 커다란 이방성이 관찰됩니다.
이러한 이방성을 이용하여 높은 열전특성과 높은 기계적 강도를 갖는 열간 프레스 법에 많은 연구가 진행되고 있습니다. 그러나 열간프레스 법에 의한 제조 방법에 있어서도 절단의 공정에 의한 생산성 저하와 제조원가 상승 등은 실용화 측면에서 큰 결점으로 남아있습니다.
전기전도도
전자전도성 반도채의 전기전도도는 식 (2.20)과 같이 나타낼 수 있습니다.
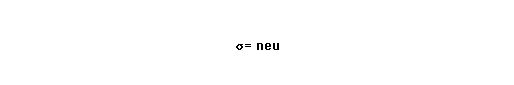
[식( 2 - 20 )]
여기서, n은 전하의 농도, e는 단위 전하량, u는 전하의 이동도 입니다. 전하의 농도는 온도의 증가에 따라 Fig. 2-6과 같이 세 영역으로 구분되어 나타난다, 영역 Ⅰ은 진성반도체의 결함들이 열에너지에 의해 이온화되는 영역으로서 전하의 농도가 온도에 따라 증가하는데 주로 저온에서 나타나다. 영역Ⅱ는 전하의 농도가 완전히 이온화된 자체의 결함농도에 의해 고정되는 extninsic 영역입니다. 영역 Ⅲ은 열 에너지에 의해 전자-전공 쌍이 생겨 전하의 농도가 온도에 따라 지수 함수적으로 증가하는 intrinsic 영역입니다. extninsic 영역에서는 전하의 농도가 거의 일정하다고 볼 수 있으므로 전기전도도는 이동 도만의 함수로 나타난다. 전하의 이동도는 결정 내에 존재하는 결함보다는 격자진동과 이온화된 impurity에 의한 사항 일 경우, 온도의 1/2승에 비례합니다.
열전도도
원자의 삼차원주기적 배열을 가진 결정질 재료 내에서 열에너지의 전달은 일반적으로 포논 (phonon), 자유전자 또는 전공(free electron or hole), 전자와 정공의 쌍, ecxiton (bound electron-hole pair),photon(radiant energy)등의 매체에 의해서 이루어지며, 재료가 도체인 경우에는 일반적으로 위에 기술한 여러 가지 매체중 열전도에 크게 기여하는 전하(ccarrier)와 포논만을 고려합니다.[26]. 이에 따라 재료의 열전도 도는 식 (2.21)과 같이 나타낼수 있습니다.

[식( 2 - 21 )]
식(2.21)에서 ktot는 전체 열전도도, ke은 carrier에 의한 열전도도, kph은격자진동에 의한 열전도 도로써 포논이란 결정 내에서의 격자진동을 양자화 시킨 것으로 가상적인 입자로 생각합니다. 포 논의 산란은 다른 포논과의 충돌, 전자와의 상호작용 및 격자 결함에 의해 발생합니다. 격자 열전도도에 영향을 미치는 주요 결함의형태로는 결정립계, 전위, 합금과 불순물의 고용 등에 의해 발생하는 격자 변형을 들수 있습니다. 포논-포논 산란은 저온계 에서는 매우 약하기 때문에 저온에서는 격자 결함에 의한 포논 산란이 지배적으로 작용합니다. 이와 같은 포논 산란처는 전하의 산란을 유발하기 때문에 전하에 의한 열전도도 ke에도 영향을 미치며 전기 전기 전기 전도도에도 영향을 미친다. 이러한 전하에 의한 열전도도와 전기전도도 사이에는 고전 전자이론의 가장 중요한 결과중의 하나인 Wiedeman-fRANZ 법칙이 성립하여 [20-22], 전하의 농도가 적은 nondegenerate semiconductor의 경우 식(2.22)와 같이 표현되며 전하의 농도가 충분히 많은 degenerate semiconductor에서는 식 (2.23)으로 표현됩니다.
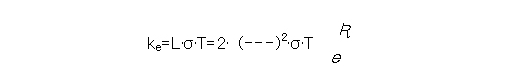
[식( 2 - 22 )]
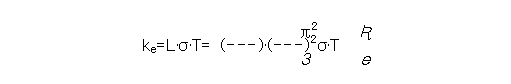
[식( 2 - 23 )]
여기서, k는 Boltzmann 상수, Lorenz 상수입니다.

